この曲面は1864年、 アルフレッド・エンネパー (英語版、ドイツ語版) によって 極小曲面 (英語版) 理論との関わりから導入された 。 ワイエルシュトラス–エンネパーの媒介変数表示 (英語版) は非常に簡単で、 =, = となる。実変数での媒介変数表示はこの式から容易に計算できる。§1 極小曲面 §2 極小曲面の例 §3 複素関数論の準備(1) §4曲面の等温座標 §5エンネパーの公式 §6随伴極小曲面 §7極小曲面の第2基本量 §8懸垂曲面と常らせん面 §9 懸垂曲面と常らせん面(2) §10エンネパー極小曲面 §11シェルク極小曲面 §12その他の極小曲面図1 カテノイドと呼ばれる極小曲面の形をしている。 図2、図3 2つの曲面の形は違うものの、面積はほぼ等しい。 図4 トリプルジャンクションを含む極小曲面の図。

一個直觀而複雜的難題 追求 極小 每日頭條
極小曲面 変分
極小曲面 変分-Mar 23, 11 · 平均曲率が至る所0の曲面は極小曲面とも呼ばれ、与えられた境界条件での面積最小の曲面(境界があるシャボン玉の局面)になります。 参考文献 Crandall, Mathematica―理工系ツールとしての (アジソン ウェスレイ・トッパン情報科学シリーズ) p54p57Gauss曲率が一定な極小曲面は平面に限る 回転面で極小曲面となるのは平面と懸垂面に限る(O Bonnet, 1860) 線織面で極小曲面となるのは平面と常螺旋面に限る (E Catalan, 1842) 移動曲面で極小曲面となるのは平面とScherkの2重周期的曲面に限 る(H Scherk, 15)



ストッキングを使った極小曲面 最小面積曲面の実験 とね日記
のエンドをもつ極小曲面で 3 つ以上 Osserman 不等式の等号をみたす例は多 く知られているが, 2 つのエンドをもつ極小曲面で等号をみたすもの は懸垂面に限られることが知られている 本稿では, 2 つのエンドを もつ極小曲面とその全曲率について考察する 11 極小曲面を用いた量子ナノ構造 東北大学・多元物質科学研究所 藤田 伸尚 1.はじめに 自然界に見られる安定な物質構造の多くは、与えられた温度・圧力・化学ポテンシャル等の条21 シャボン膜の数学への序文— シャボン膜と極小曲面— 22 平面曲線の曲率 23 曲面の平均曲率— 極小曲面の曲がり具合いによる特徴付け— 24 極小曲面の例 25 極小曲面を研究する方法の一端 26 WeierstarssEnneper の表現公式 27 同じ枠を張る石鹸膜の個数
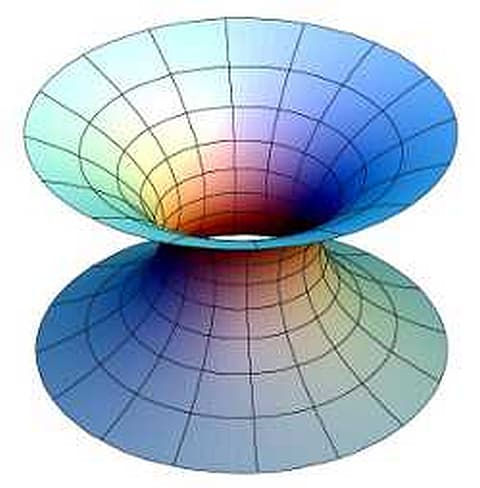
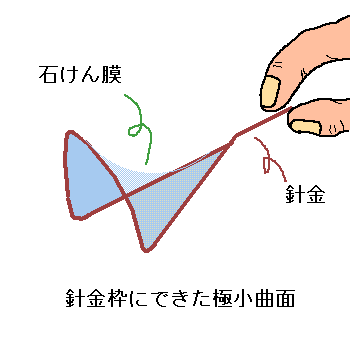
Mar 31, 17 · しかし、このシャボン玉には表面積を最小に保とうとする性質があり、遊びの域を越えて シャボン玉は、極小曲面という数学的問題の物理的な具体例になっています。 沖縄科学技術大学院大学(OIST)の研究員らは、柔軟性のある枠に張られた石けん膜をを極小にする関数y = y(x) を求めれば良い。 シャボン玉のように、石けん水でできる膜の面は面積が最小である。向かい 合った二つの円を石けん水につけてできる膜が上の極小曲面である。(ただし細 かいことをいえば、極小曲面が必ずしも面積最小では内の極小曲面である.d = 1のときを一重周期極小曲面,d = 2のときを二重 周期極小曲面,d = 3 のときを三重周期極小曲面という. 次に,極小はめ込みf M !
R3=G に対する表現公式を与える.M には 誘導計量に適合する等温座標によってRiemann面の構造を入れる(1)と同値な式(極小曲面の方程式)を導いた(1776): 1f2 y f xx −2f xf yf xy 1f2 x f yy = 0 (2) (2)が,曲面z = f(x,y)の平均曲率が0であることと同値である ことを示した.その後,平均曲率が至るところ0 であるような曲面 が極小曲面と呼ばれるようになった.それゆえに$h=0$の曲面を極小曲面といいます. まず,平均曲率$H$の復習から始めましょう. 曲面$S\boldsymbol{f}(u,v)=(f^1(u,v),f^2(u,v),f^3(u,v))$ の点$P$における法曲率$k_n$ の最大値,最小値をそれぞれ$k_1,k_2$ とする.



プラトーの問題 というのは 数学的な 極小曲面



シャボン玉 枠 極小曲面 物理学 幾何学 十二面体 の画像素材 写真素材ならイメージナビ
= a z2 dz を考える.ただしa 2 C は零でない定数.これらをワイエルストラス表現公式 (51) f(z) = Re ∫ z z0 (1 g2);極小曲面 Sy = ∫a 0 y √ 1y′2 dx 最速降下線:Ty = ∫a 0 p 1y′2 p y dx このような問題を解く数学的な方法が変分法である。関数y(x) が極値をとる xの値を求める方法が微分法であるのに対し、汎関数Iyが極値をとる関数y(x) を求める方法が変分法である。極小曲面は,石鹸膜の数学的なモデルです. 与えられた枠に膜を張るときに その面積を小さくしようとする力が働くとします. 極小曲面はそのとき出来上がる形と思ってください. 枠をねじまげると,できる曲面の形も複雑になることが想像できます.




熱賣現代極小曲面講義澤維爾 潮小李高等教育出版社現代數學基礎極小曲面的gauss映射calabi猜想以及ca 露天拍賣




微分 幾何 517 極小曲面 2 Deutschhk 的部落格 Udn部落格
3 極小曲面方程式とLaplace 方程式 針金などで境界をつくったシャボンの膜は表面積が最 小となるように張られる.そのような曲面を定める問題 をPlateau 問題といい,この問題も曲面の汎関数を考え ることで定式化することができる.ここではD ˆ R2 で特異点を持つ時間的極小曲面のガウス曲率について 赤嶺 新太郎 (九州大学大学院数理学府) 概 要 3次元ローレンツ・ミンコフスキー空間内の時間的曲面は,ローレンツ計量 を持つため,曲面の主曲率が実数になるとは限らないという性質がある.本(3) 極小曲面としゃぼん膜北畑裕之・小磯深幸 63 ・数と論理の物語――不完全性定理について考えるための10の定理 タルスキの定理/実閉順序体の量化子除去菊池 誠 70 ・双対と表現/誘導表現梅田 亨 77 ****



漲姿勢 肥皂泡泡背後隱藏的幾何魅力 雪花新闻




号 極小曲面ゴルフボール部品 Astamuse
骨子 1 曲面の幾何学 2 周期的極小曲面 3 曲面に拘束された電子 4 p, d, g 表面のバンド構造 5 波動銫数の対称性とノード線210 位相的極小曲面 28 4 第II部 結び目の位置と基本定理 29時間的極小曲面の特異点とガウス曲率 赤嶺新太郎(Shintaro AKAMINE) 九州大学大学院数理学府数理学専攻 概要 3 次元ローレンツ・ミンコフスキー空間L3 内の時間的極小曲面のガウス曲率の符号(実および複素主曲 率の有無) が,曲面を構成する2 つのナル曲線の退化性と向きだけで決まることを証明し




ストッキングを使った極小曲面 最小面積曲面の実験 とね日記




極小曲面入門 19年 03 月号 雑誌 数理科学 別冊 本 通販 Amazon
極小曲面で回転面であるものを求めてみよう。H = 0 より、常 微分方程式 h(x)h′′(x) − h′(x)2 − 1 = 0 を解けばよい。曲面を考えているので、h(t) ̸= 0 のところで考え る。解h(t) がC2 級ならば、h′′(x) = (h′(x)2 1)/h(t) より自動 的にC3 級となることに注意して、方程式の両辺を微分すると、10 年11 月2 日 山田光太郎 kotaro@mathtitechacjp 幾何学特論第二講義資料5 5 極小曲面の例 = C nf0g 上の正則関数g と正則1 次微分形式 g(z) = z;極小曲面の場合は Liouville 方程式 $u_{z\overline{z}}2e^{u}=0$ になるような $z$ をとることができる Liouville 方程式は一般解を与える公式が存在する その事実の反映とし て極小曲面の積分表示式が




ストッキングを使った極小曲面 最小面積曲面の実験 とね日記




ストッキングを使った極小曲面 最小面積曲面の実験 とね日記
Mar 24, 19 · 極小曲面論入門 その幾何学的性質を探る 川上裕・藤森祥一 共著 19年3月25日 初版発行 極小(超)局面の基礎 を 次元多様体とする。 はめ込み のことを の超曲面という。 特に、 のときは の曲面という。 の第一基本形式 の逆行列 の 成分を で表す。Mar 11, 21 · また, 極小曲面の描画に関してはWeber氏以外にもPeter Connor氏, 小林真平氏, Wayne Rossman氏, SeongDeog Yang氏から有益なご意見をいただきました ここに記して感謝の意を表しまMay 25, 21 · また, 極小曲面の描画に関してはWeber氏以外にもPeter Connor氏, 小林真平氏, 中村英史氏, Wayne Rossman氏, SeongDeog Yang氏から有益なご意見をいただきました ここに記して感謝の意を表します Links Minimal Surface Repository (Matthias Weber氏)



シャボン玉 枠 極小曲面 立方体 物理学 幾何学 の画像素材 写真素材ならイメージナビ




流動的美麗 極小曲面的製作 Getit01
うな曲面を, 一般に極小曲面と 呼ばれている 先の表で言うと, シャボン玉のように空気を包み こんでできる曲面ではなく, 輪 を縁として張る面積極小の曲面 のことである (写真は, u 字形針金輪に樹脂膜を張らせて固めた もの)極小曲面とは? 空間内にに与えられた一つの閉曲線で囲まれた曲面のうち面積最小のもの を 「極小曲面」 と言う。 極小曲面の上ではどこでも 平均曲率が0 である。きょくしょうきょくめん極小曲面 minimal surface Sを 曲面 とし, P をその1点とする。 PにおけるSの法線 (PにおいてSに立てた 垂線 )を含むすべての 平面 を考え,これらの平面によるSの 切口 である 曲線 の 曲率 (≧0)に,法線のある向きに関して曲線が 凹 であるか 凸 であるかに応じて正負の 符号 をつける。 このとき,これらの最大値と最小値の和が0となるなら



Udag




10年度 数理科学総論
A03 「極小曲面とナノ構造の動的構造形成」 対象とする物質 複合材料、特に触媒 b01「物質・材料科学のための情報科学基盤」 ネットワーク解析、画像解析、機械学習極小曲面・定平均曲率曲面 ガウス曲率一定曲面 極小曲面 平均曲率一定曲面 面積最小の曲面 平均曲率が恒等的に 0 である曲面を 極小曲面 という. 事実 与えられた境界をもつ曲面のうち,最小の面積をもつものは極小 曲面である. 石鹸膜の形は極小曲面極小曲面とは曲面積が変形によって極小(極大)になるような曲面である. 卒業研究では極小曲面に関する次のような研究を行った.主結果は以下の2 つである. (1) 曲面sのε変形を考えて,その面積をa(ε) と表し,変分法によりa(ε) の一階微




3重周期的極小曲面




這種新材料 未來可能作為骨頭植入你體內 虎嗅網 Mdeditor
セミナーでは 小林昭七,曲線と曲面の微分幾何(改訂版),裳華房 の第5章を使って、3次元ユークリッド空間内の極小曲面について勉強しました。 任意の単連結な極小曲面はWeierstrassEnneperの表現公式によって正則ポテンシャルから構成されることを学びさて,極小曲面の研究の歴史は,JLLagrange が``Essai d'une nouvelle methode pour determiner les maxima et les minima des formules integrales indefinies'' (1762) の中で,極値問題の例として 「 内に与えられた1つの閉曲線に対し,これを境界にもつ曲面全体の中 で面積最小のものを納谷 信 (名古屋大学・教授、極小曲面論・平均曲率一定曲面論) 研究協力者 松江 要 (九州大学・特任助教) 小磯 深幸 (九州大学・教授) 赤嶺 新太郎 (日本大学生物資源学部・助教) 五明 工 (名古屋大学多元数理科学研究科・特任助教)



極小曲面 Youtube




極小曲面之亭 日本 壹讀
極小曲面や極大曲面は複素座標系に対する座標関数が(それぞれの誘導計量に関して)調和 関数であるという特徴付けを持つ.したがって,複素座標表示された極小曲面Xmin(w) = (x(w);y(w);t(w))に対して,それらの座標関数の共役調和関数を取って得られる曲面X




極小曲面之亭 日本 壹讀




微分 幾何 517 極小曲面 2 Deutschhk 的部落格 Udn相簿




号 極小曲面ゴルフボール部品 Astamuse




シェルク極小曲面風ペン立て Dmm Make クリエイターズマーケット



ストッキングを使った極小曲面 最小面積曲面の実験 とね日記




シェルク極小曲面風ペン立て Dmm Make クリエイターズマーケット



集中講義 極小曲面入門 Furuhata




流動的美麗 極小曲面的製作 Getit01




極小曲面 物理學概念 在數學中 極小曲面是指平均曲率為 華人百科




号 極小曲面ゴルフボール部品 Astamuse




号 極小曲面ゴルフボール部品 Astamuse




曲面 維基百科 自由的百科全書



微分幾何




這種新材料 未來可能作為骨頭植入你體內 虎嗅網 Mdeditor



微分幾何




流動的美麗 極小曲面的製作 Getit01




極小曲面 藤森祥一




流動的美麗 極小曲面的製作 Getit01



螺旋曲面 维基百科 自由的百科全书




Tsujimotter ロマ数本好評発売中 Auf Twitter 昨日の懇親会でほりたみゅ君 Hyrodium が持ってきた作品を見せてもらいました 2つの円周をつなぐ極小曲面 面積最小の曲面 写真左 と螺旋 写真右 はガウス曲率が等しいので こんな風に互いに変形できるんです




極小曲面 簡體書 三民網路書店




極小曲面 Wikiwand



ストッキングを使った極小曲面 最小面積曲面の実験 とね日記



Enneperの極小曲面




博客來 極小曲面



17年10月04日の記事 Metatronic Metalogue




數學中的驚艷美 2 看到後您不再認為數學就是一堆枯燥的公式
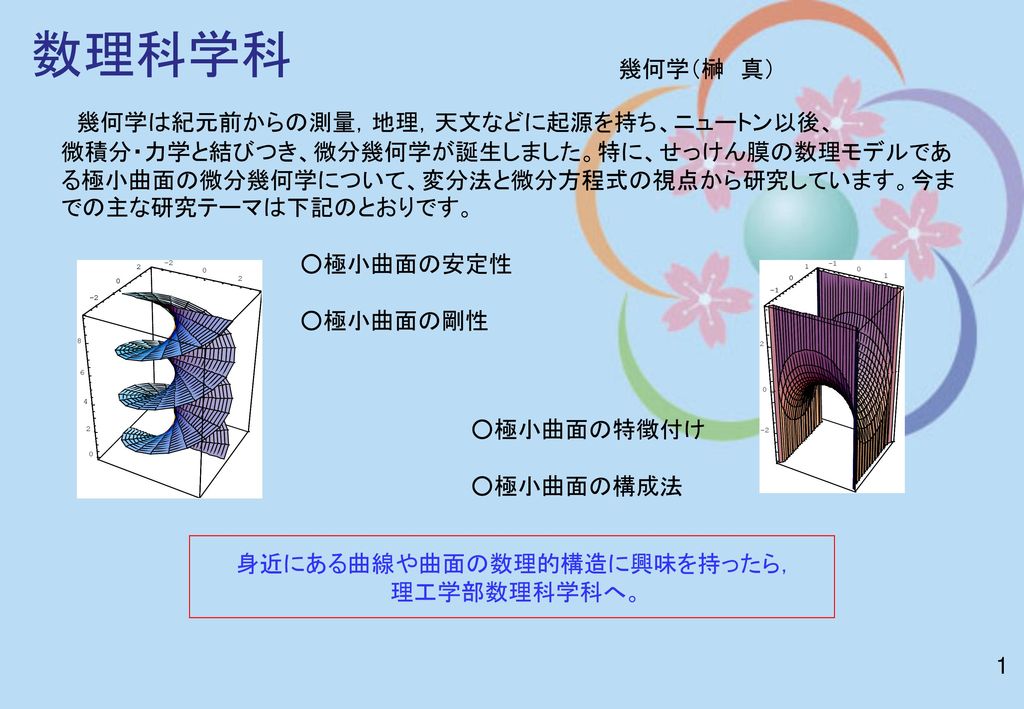



身近にある曲線や曲面の数理的構造に興味を持ったら Ppt Download




3重周期的極小曲面




流動空間 Rheotomic曲面幾何設計 每日頭條




三星s21 Ultra最新曝光 螢幕開孔極小 曲面設計 壹讀




トピックス 富山大学理学部



流動的美麗 極小曲面的製作 雪花新闻



微分幾何



Curvatureanalysis




The Aslo Booth Was Jammed With Attendees For Most Of The Two Day Festival Download Scientific Diagram



集中講義 極小曲面入門 Furuhata




極小曲面 物理學概念 在數學中 極小曲面是指平均曲率為 華人百科



魏爾斯特拉斯 恩內佩爾曲面 Wikiwand




流動的美麗 極小曲面的製作 Getit01




プラトーの問題 というのは 数学的な 極小曲面
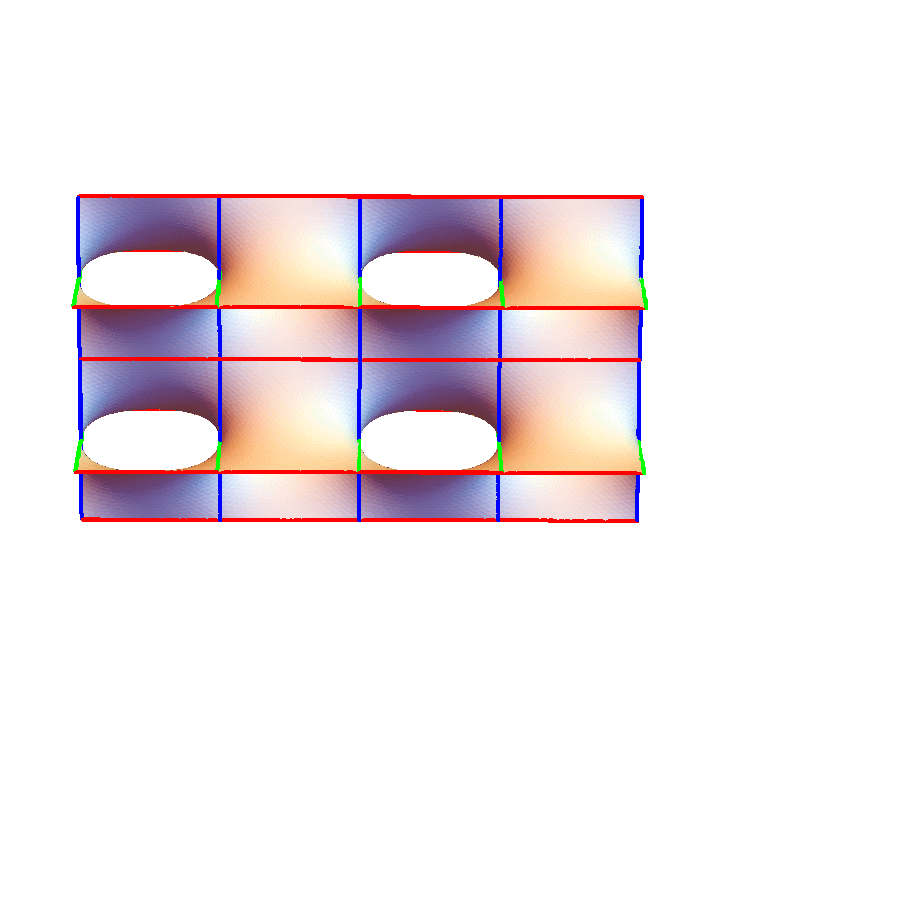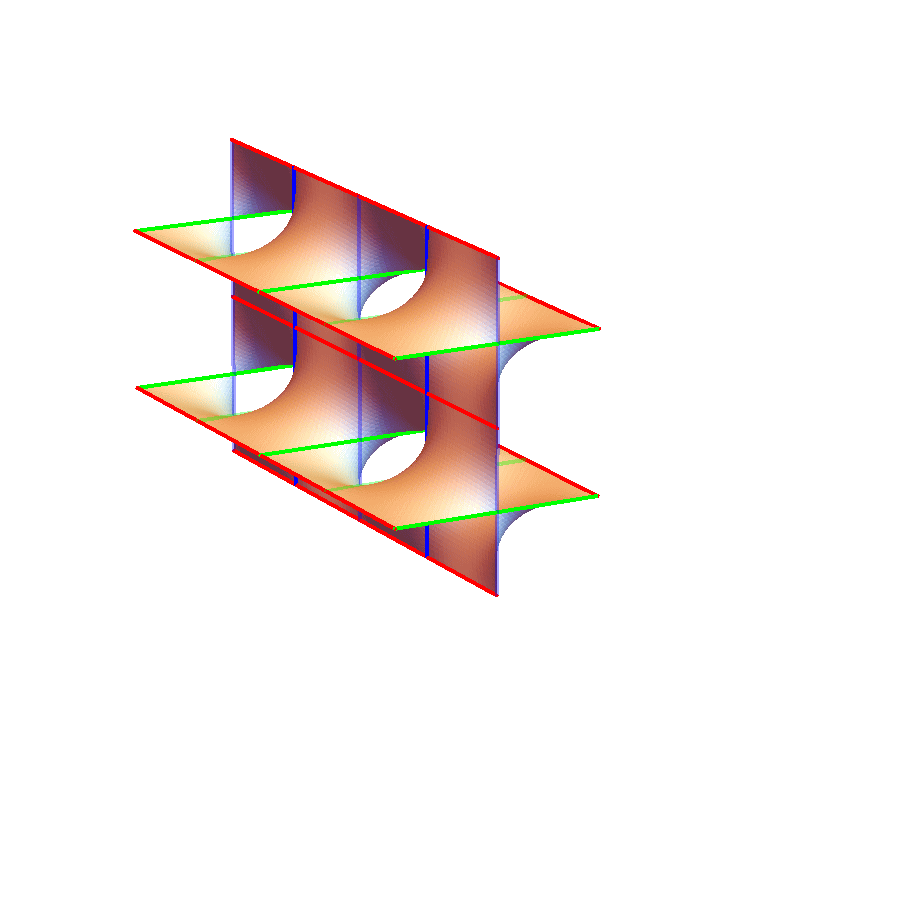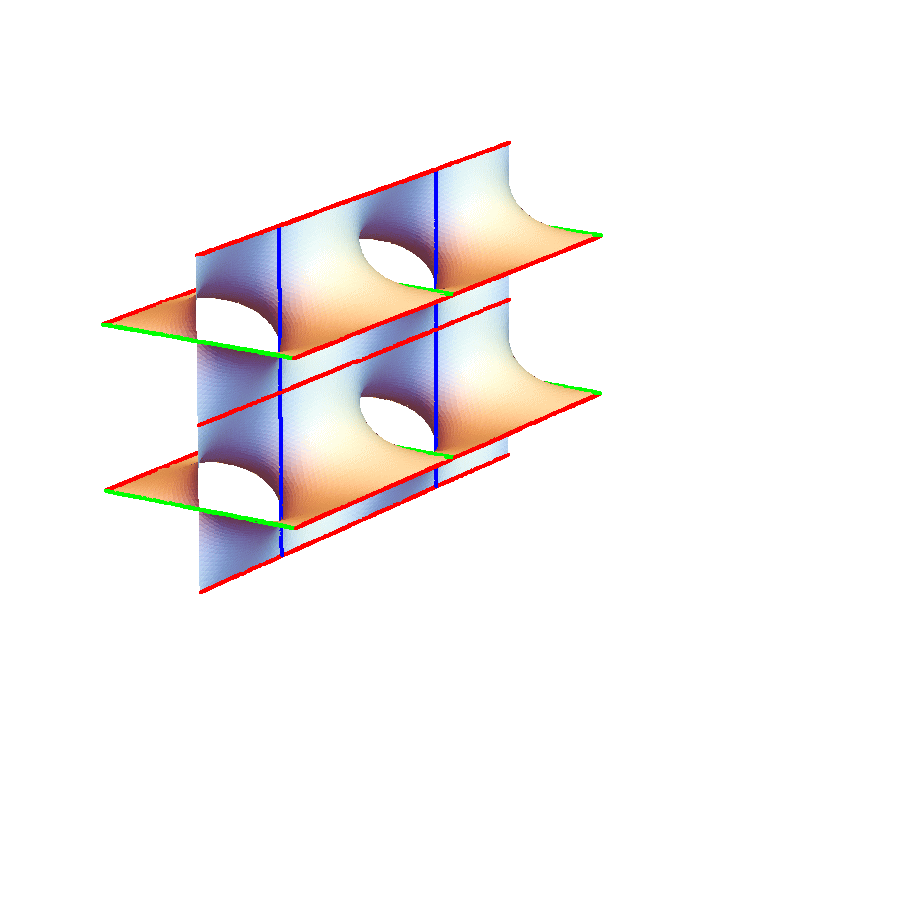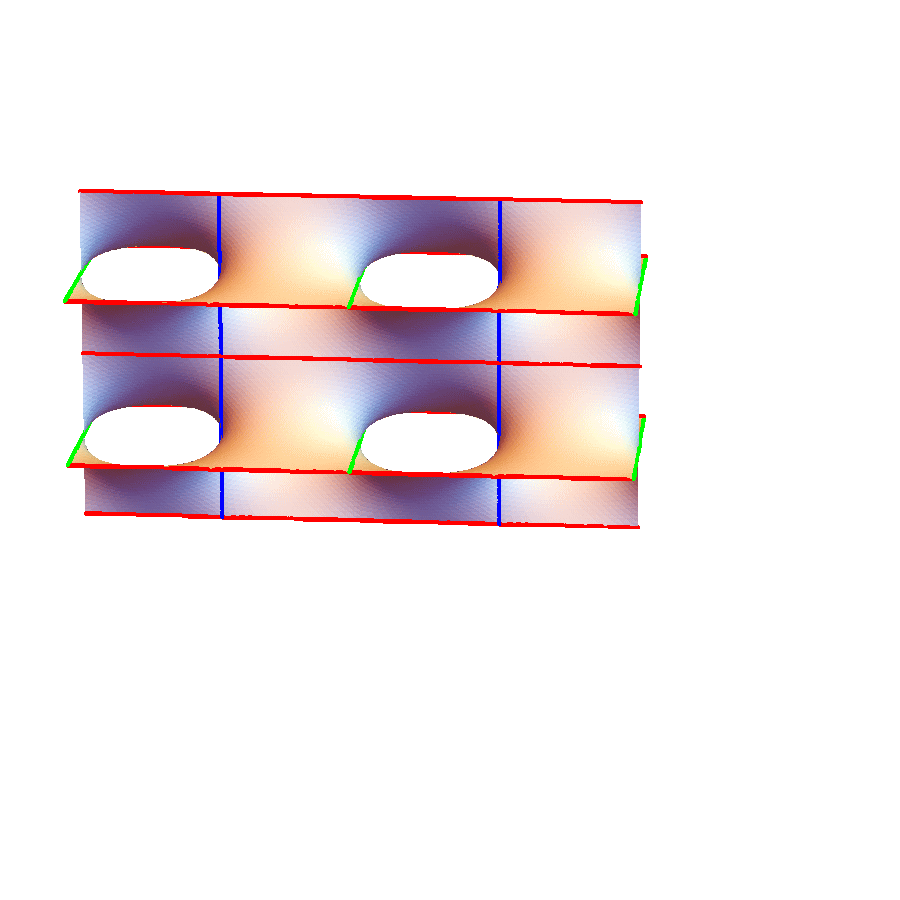



3重周期的極小曲面




正螺面 正螺面 Circular Helicoid 即正螺旋面 是一種 百科知識中文網




流動的美麗 極小曲面的製作 Getit01




流動的美麗 極小曲面的製作 Getit01



微分幾何



微分幾何




我的数学之路 丘成桐




ストッキングを使った極小曲面 最小面積曲面の実験 とね日記




參數化設計探討2 方格子




博客來 極小曲面




數學中的驚艷美 2 看到後您不再認為數學就是一




3重周期的極小曲面



集中講義 極小曲面入門 Furuhata



プラトーの極小曲面法則 その2




1 シャークの極小曲面 涼風我談の鱗




微分 幾何 518 極小曲面 3 Deutschhk 的部落格 Udn相簿



大阪大学いちょう祭 数学教室



微分幾何




現代極小曲面講義 Taaze 讀冊生活




号 極小曲面ゴルフボール部品 Astamuse




流動的美麗 極小曲面的製作 Getit01




這個簡單的圖形 為何讓最傑出的數學家和建築師最著迷 Itw01



Curvature



Udag




一個直觀而複雜的難題 追求 極小 每日頭條




10年度 数理科学総論




学位請求論文 付録b 2 極小曲面




極小曲面 維基百科 自由的百科全書




博客來 極小曲面




流動的美麗 極小曲面的製作 Getit01




極小曲面 Dvi Pdf 無料ダウンロード




平均曲率 Wikiwand



大阪大学いちょう祭 数学教室




主曲率 維基百科 自由的百科全書
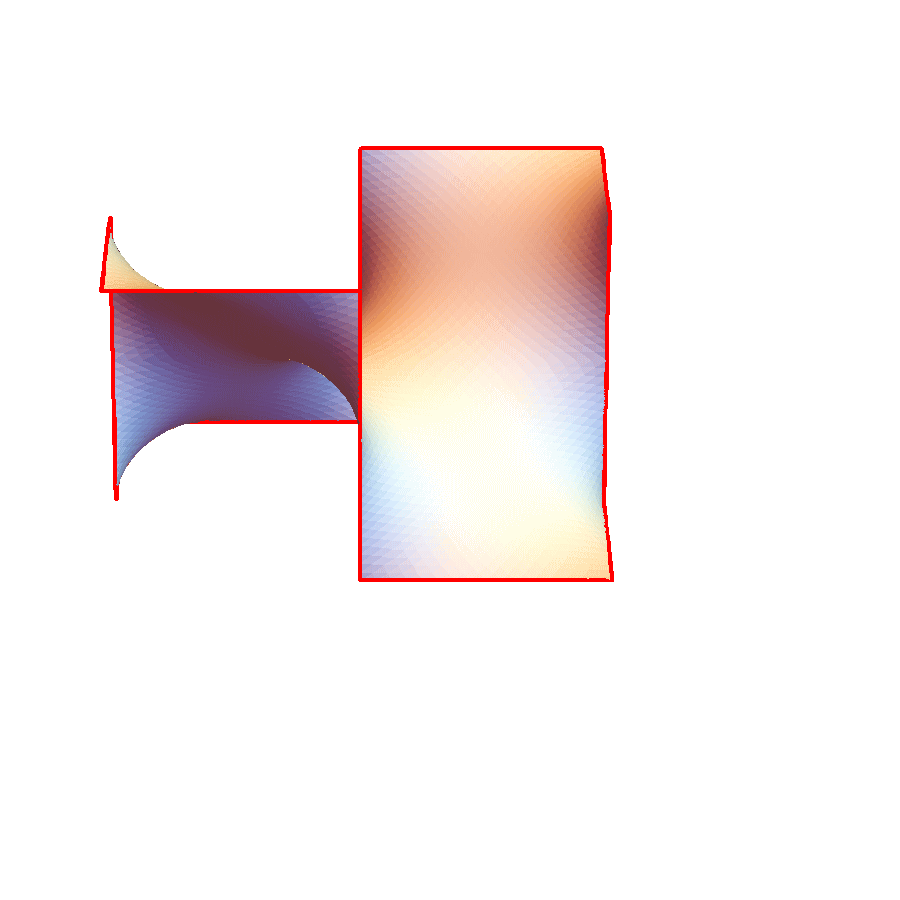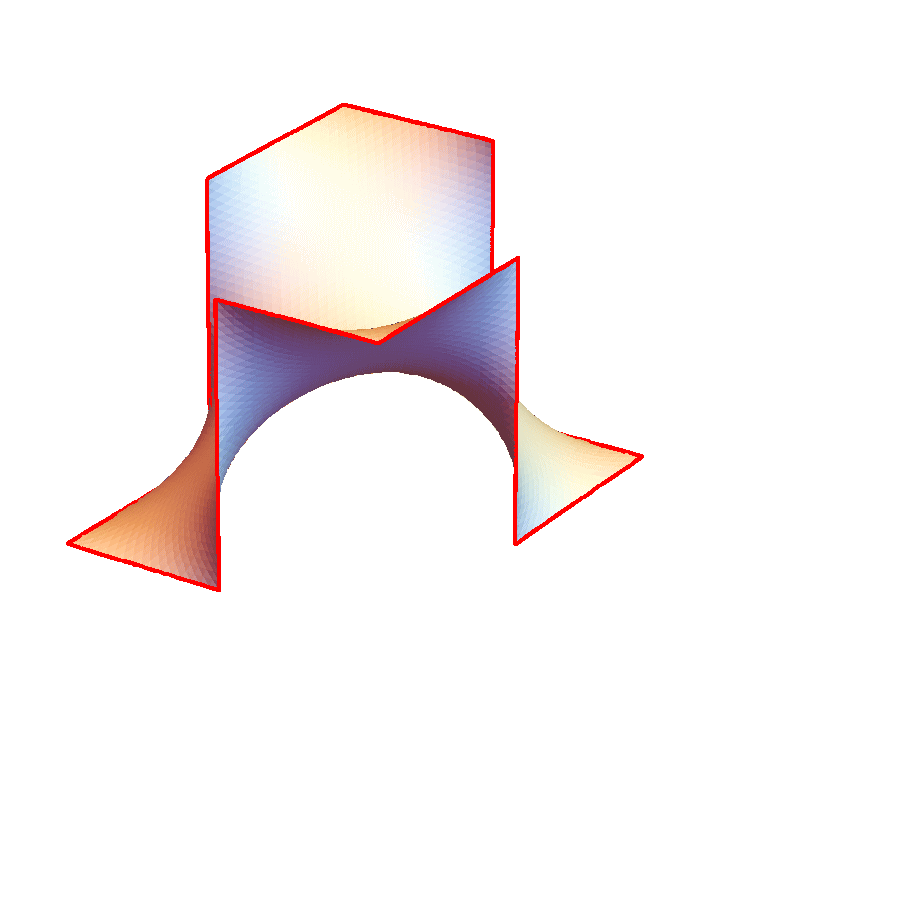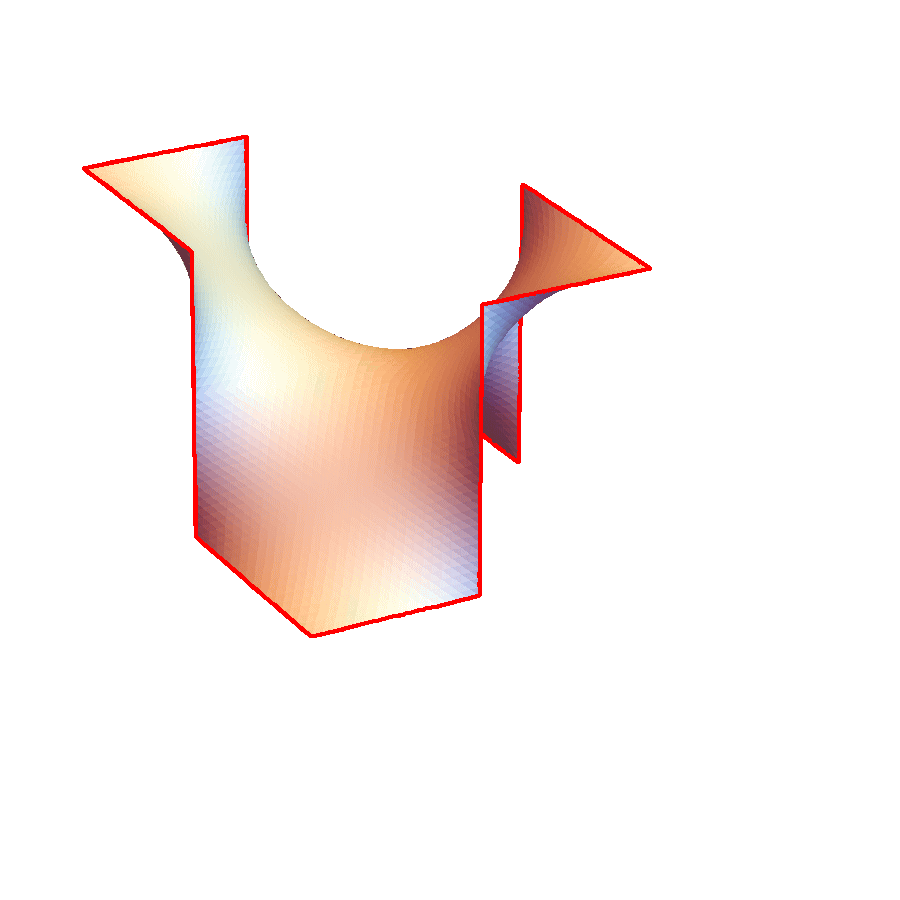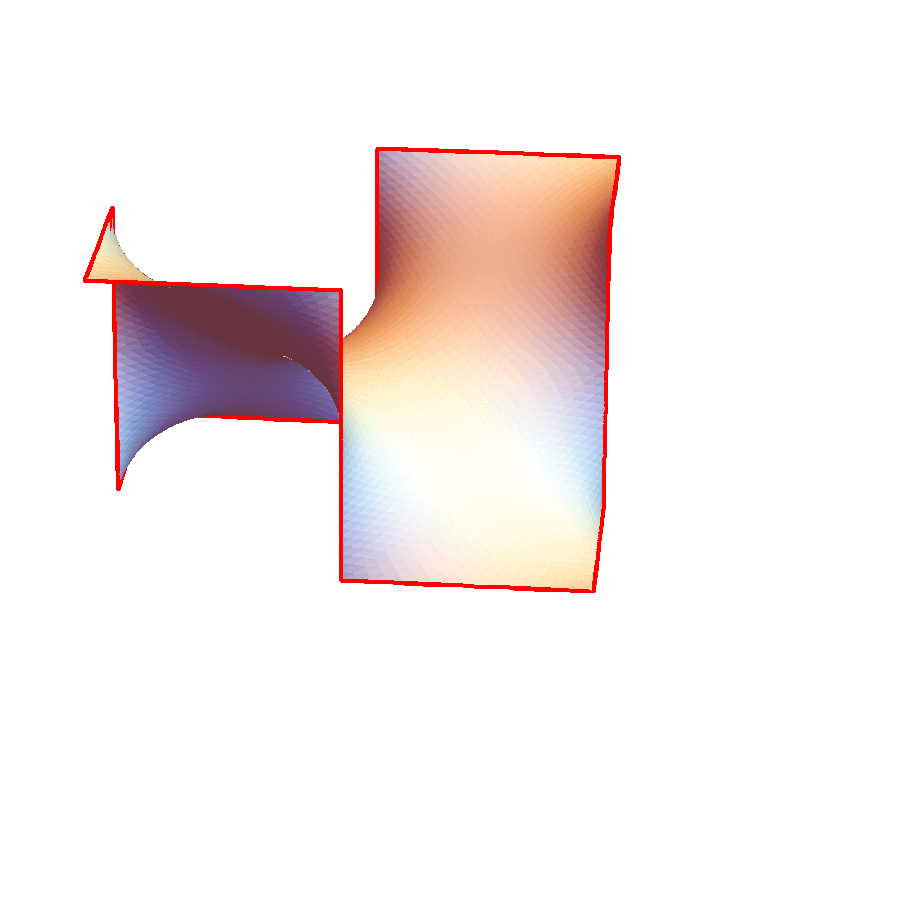



3重周期的極小曲面


0 件のコメント:
コメントを投稿